Rappels - Loi de Bernouilli et loi binomiale
- Reconnaître des situations relevant de la loi binomiale
- Calculer une probabilité dans le cadre de la loi binomiale
- Représenter la répétition d'expériences identiques et indépendantes à l'aide d'un arbre pondéré
ILoi de Bernoulli
Une expérience aléatoire avec deux issues, succés de probabilité \(p\) ou échec de probabilité \(1 - p\) est appelé une épreuve de Bernouilli de paramètre \(p\).
- Tirer à pile ou face (pile étant le succés) est une épreuve de Bernouilli de paramètre \(0,5\)
- Lancer un dé (faire \(6\) étant le succés) est une épreuve de Bernouilli de paramètre \(\frac{1}{6}\)
Une épreuve de Bernoulli peut être représentée par un arbre pondéré simple. En prenant l'exemple du dé :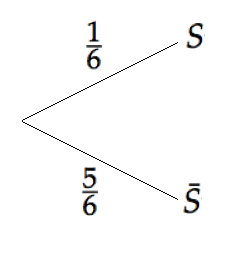 
IISchéma de Bernoulli et loi binomiale
1Schéma de Bernoulli
- Un schéma de Bernoulli d’ordre \(n\) et de paramètre \(p\) est la répétition d’une épreuve de Bernoulli de paramètre \(p\) \(n\) fois où chaque issue est indépendante.
- La loi de probabilité de la variable \(X\) comptant le nombre de succés de ce shéma de Bernouilli s'appelle la loi Binomiale et se note \(\mathcal{B}(n,p)\).
Tirer un dé (faire \(6\) étant le succés) trois fois d'affilée est un schéma de Bernouilli d'ordre 3 et de paramètre \(\frac{1}{6}\). On peu le représenter par l'arbre pondéré suivant :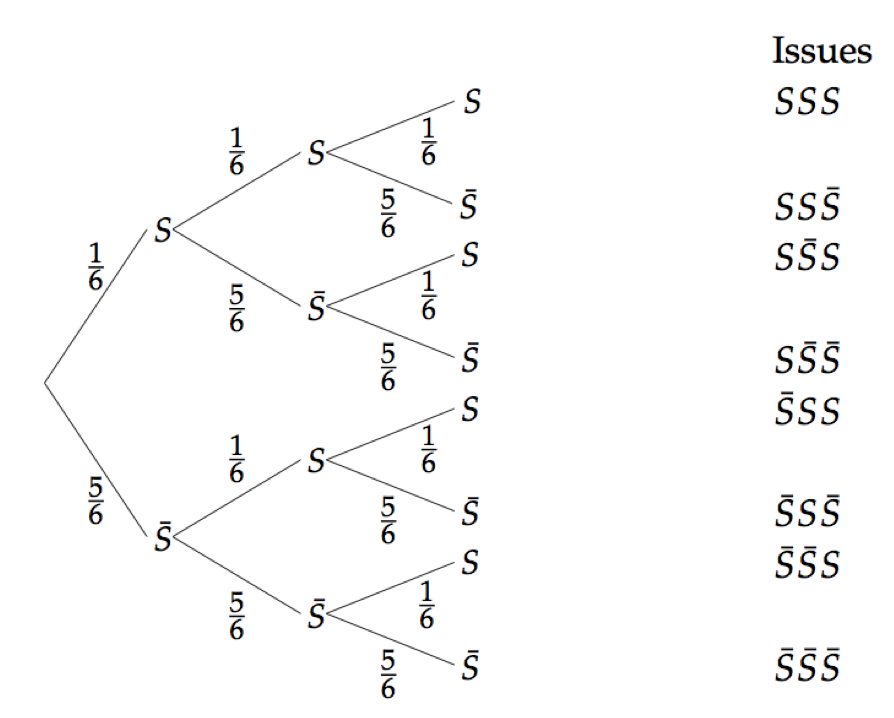 
La probabilité de gagner 2 fois \(P (X=2)\)correspond aux chemins dans l'arbre : \(SS\bar{S}\) ou \(S\bar{S}S\) ou \(SS\bar{S}\) ou \(\bar{S}SS\) : $$ \begin{array}{lll} P (X=2) &=& (\frac{1}{6}\times\frac{1}{6}\times\frac{5}{6}) + (\frac{1}{6}\times\frac{5}{6}\times\frac{1}{6}) + (\frac{5}{6}\times\frac{1}{6}\times\frac{1}{6}) \\ &=& \text{nombre de chemins à deux succés} \times (\frac{1}{6})^2\times (\frac{5}{6})^1 \end{array} $$
La probabilité de gagner 2 fois \(P (X=2)\)correspond aux chemins dans l'arbre : \(SS\bar{S}\) ou \(S\bar{S}S\) ou \(SS\bar{S}\) ou \(\bar{S}SS\) : $$ \begin{array}{lll} P (X=2) &=& (\frac{1}{6}\times\frac{1}{6}\times\frac{5}{6}) + (\frac{1}{6}\times\frac{5}{6}\times\frac{1}{6}) + (\frac{5}{6}\times\frac{1}{6}\times\frac{1}{6}) \\ &=& \text{nombre de chemins à deux succés} \times (\frac{1}{6})^2\times (\frac{5}{6})^1 \end{array} $$
2Coefficients binomiaux et loi binomiale
Le coefficient binomial \(\binom{n}{k}\) est le nombre de chemins réalisant \(k\) succés pour \(n\) répétitions.
Dans l'exemple précédent, le nombre de chemins à \(2\) succés parmi \(3\) tirs est \(\binom{2}{3} = 3\)
À la calculatrice, on peut calculer \(\binom{n}{k}\) de la manière suivante :
-
Texas Instrument : touche MATH puis PRB, puis Combinaison. On tape
n Combinaison k -
Casio : touce OPTN puis →, puis PROB puis nCr. On tape
n nCr k
La probabilité de faire \(k\) succés parmi \(n\) dans une épreuve de Bernouilli de paramètre \(p\) est : $$ P (X = k) = \binom{n}{k} p^k \times (1-p)^{n-k} $$
À la calculatrice, on peut calculer \(P (X=k)\) pour la loi binomiale\(\mathcal{B}(n,p)\) de la manière suivante :
-
Texas Instrument : Menu Distrib (2nde+Var) puis PRB, puis BinomFdp. On tape
BinomFdp (n,p,k) -
Casio : touche OPTN puis STAT, puis DIST puis BINM puis Bpd. On tape
BinomialPD (k, n, p)
À la calculatrice, on peut calculer \(P (X\leq k)\) pour la loi binomiale\(\mathcal{B}(n,p)\) de la manière suivante :
-
Texas Instrument : Menu Distrib (2nde+Var) puis PRB, puis BinomFRép. On tape
BinomFRép (n,p,k) -
Casio : touche OPTN puis STAT, puis DIST puis BINM puis Bcd. On tape
BinomialCD (k, n, p)
IIIEspérance, écart type
On considère une variable aléatoire \(X\) suivant une loi binomiale \(\mathcal{B}(n,p)\) :
- Son espérance \(E (X) = n p\)
- Son écart type \(\sigma = \sqrt{n p (1-p)}\)
L'espérance représente la valeur moyenne prise par la variable aléatoire. L'écart type représente l'écart moyen entre deux valeurs prises par la variable aléatoire.